Task

使用上一篇讲述到的代码做一个MNIST的手写数字分类的模型：能够做多类别分类来识别任何数字。
给train data和test data计算准确率，输出confusion矩阵

Hint

1、对每一个数字：创建一个二元分类器： this digit vs all other digit
2、给每一个数字创建不同的二元分类感受器
3、定义一个函数来分类输入的数字

如果外面将10个感受器的权重合到一个矩阵上，我们就能将10个感受器的结果通过一次矩阵乘法完成。最可能的数字将通过argmax操作输出出来

Think

前文Perceptron一节中我们构建了一个二元的分类器，即可以分辨两个数字的的神经网络，那么我们分辨10个数字的神经网络便在此基础上来改造
最直接的想法就是提示中给我们的思路：仍然使用一个二元分类器，用于分类这个数字和其他数字
于是乎答案呼之欲出了，我们仍然用一个特定的数字i来作为这个数字的数据，对于其他数字的数据，我们则将0~9中除了i以外的所有数字的数据混合在一起，就得到了其他数字的数据集，随后我们用同样的方法训练一个二元分类器，看上去我们的任务就将圆满完成了！！

Let’s do it

neccessary lib

1
2
3
4
5
6
import matplotlib.pyplot as plt
import numpy as np
import pickle
import gzip
import os
import random

copy functions

我们直接把Perceptron中的训练函数摘抄过来

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def train(positive_examples, negative_examples, num_iterations = 100):
    num_dims = positive_examples.shape[1]
    weights = np.zeros((num_dims,1)) # initialize weights
    
    pos_count = positive_examples.shape[0]
    neg_count = negative_examples.shape[0]
    
    report_frequency = 10
    
    for i in range(num_iterations):
        pos = random.choice(positive_examples)
        neg = random.choice(negative_examples)

        z = np.dot(pos, weights)   
        if z < 0:
            weights = weights + pos.reshape(weights.shape)

        z  = np.dot(neg, weights)
        if z >= 0:
            weights = weights - neg.reshape(weights.shape)
            
        if i % report_frequency == 0:             
            pos_out = np.dot(positive_examples, weights)
            neg_out = np.dot(negative_examples, weights)        
            pos_correct = (pos_out >= 0).sum() / float(pos_count)
            neg_correct = (neg_out < 0).sum() / float(neg_count)
            # print("Iteration={}, pos correct={}, neg correct={}".format(i,pos_correct,neg_correct))

    return weights

以及判断分类器正确率的函数

1
2
3
4
def accuracy(weights, test_x, test_labels):
    ones = np.c_[test_x,np.ones(len(test_x))]
    res = np.dot(ones , weights)
    return (res.reshape(test_labels.shape)*test_labels>=0).sum()/float(len(test_labels))

load data set

again，笔记中给出的下载代码看上去没法在win中运行，Suchan这里和Perceptron一节中一样，直接下载现成的zip文件
然后稍微替换一下dataset的加载方式

1
2
3
4
5
# with open('./mnist.pkl', 'rb') as mnist_pickle:
#     MNIST = pickle.load(mnist_pickle)
    
with gzip.open('./mnist.pkl.gz', 'rb') as mnist_pickle:
    MNIST = pickle.load(mnist_pickle)

copy一下教程对数据的处理,why not?

1
2
3
4
5
6
7
8
9
print(MNIST['Train']['Features'][0][130:180])
print(MNIST['Train']['Labels'][0])
features = MNIST['Train']['Features'].astype(np.float32) / 256.0
labels = MNIST['Train']['Labels']
fig = plt.figure(figsize=(10,5))
for i in range(10):
    ax = fig.add_subplot(1,10,i+1)
    plt.imshow(features[i].reshape(28,28))
plt.show()

process

笔记中给出了一个已有的函数

1
2
3
4
5
6
7
8
9
10
def set_mnist_pos_neg(positive_label, negative_label):
    positive_indices = [i for i, j in enumerate(MNIST['Train']['Labels']) 
                          if j == positive_label]
    negative_indices = [i for i, j in enumerate(MNIST['Train']['Labels']) 
                          if j == negative_label]

    positive_images = MNIST['Train']['Features'][positive_indices]
    negative_images = MNIST['Train']['Features'][negative_indices]

    return positive_images, negative_images

函数要求我们输入两个数字，一个这个数字 一个其他数字
但是根据前文的思路来说，我们没办法将其他数字这个概念填入到这个函数中，我们不妨改造一个函数，用于输入一个数字，获取到它的数据集即可

1
2
3
4
5
6
def get_mnist_pos(lable):
    positive_indices = [i for i, j in enumerate(MNIST['Train']['Labels']) 
                          if j == lable]
    positive_images = MNIST['Train']['Features'][positive_indices]
    
    return positive_images

最终计算准确率之前，我们还要定义一个改造数据的函数：即我们最终的测试集也需要包含这个数字和其他数字
回想我们这个架构的工作流程：对于这个数字，我们将输出一个正值，对于其他数字我们应该一个负值，那么很容易想到我们构造的label就应该是：对于当前数字我们给一个+1，对于其他数字我们给一个-1，到时候其做点乘，如果结果正确，二者点乘的结果就应该是正值

1
2
3
4
5
6
7
8
9
def gen_test_data(test_pos , test_label , this_num):#约定传入的test_poss:当前数字的数据集 ， test_label:+1 ， this_num:当前数字
    for i in range(10):
        if i == this_num:
            continue
        other_num_pos = get_mnist_pos(i)
        split_pre , split_post = np.split(other_num_pos, split_num)
        test_pos = np.concatenate((test_pos, split_post),axis=0)
        test_label = np.concatenate((test_label , np.full(split_post.shape[0] , -1)),axis=0)
    return test_pos , test_label

然后我们来对每一个数字进行一次训练，将训练出来的weight返回出去

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def train_this_num(this_num):
    this_num_pos = get_mnist_pos(this_num)#获取到当前数字的数据集
    other_num_pos = np.array([1,1])#此处算是Suchan对python语法不太熟悉，有熟悉的读者朋友可以自行修改。大致思路就是：先给other_num_pos赋一个随便什么值，在之后获取其他数字的数据集时候不断填充进其他数据
    flag = True
    for i in range(10):
        if i == this_num:
            continue
            
        tem_pos = get_mnist_pos(i)
        
        if flag:
            flag = False
            other_num_pos = tem_pos
        else:
            other_num_pos = np.concatenate((other_num_pos, tem_pos),axis=0)
            
            
    train_x , test_x = np.split(this_num_pos, [2000])#此处前一节的教程的分割方式是 train_x, test_x = np.split(X, [ n*8//10])，导致在train的时候训练集太少，测试集太多，没有拟合好，提醒各位朋友在分割数据集的时候尽量手动check一下训练集和测试集的比例
    #或者使用sklearn.model_selection下的train_test_split
    #例如：features_train, features_test, labels_train, labels_test = train_test_split(data,labels,test_size=0.2)
    train_x = np.c_[train_x,np.ones(len(train_x))]# 给输入向量添加一个高维度的1作为bias
    tain_y = np.full((train_x.shape[0]), this_num)
    test_y = np.full((test_x.shape[0]) , this_num)
    other_num_pos = np.c_[other_num_pos,np.ones(len(other_num_pos))]
    weight = train(train_x , other_num_pos , 1000)
    test_x , test_y = gen_test_data(test_x , test_y , this_num)#给当前测试集添加其他数字做正反判断
    ac = accuracy(weight, test_x, test_y)

    print("{} : accuracy = {}".format(this_num, ac))
    return weight

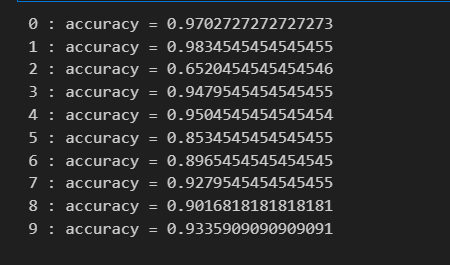
好了，经过以上代码，我们运行能够得到我们的结果：
result
看上去结果还是可以接受。

  • 至于最终定义一个函数来判断这里省略吧，其实也就是把全部的weight组合在一起，点乘输出一个向量，得到正值的就是我们的结果