ODE & SDE in Generative Models

前言：
在上一阶段的 Image Inpainting 课题中，我主要将 Diffusion Model 作为工具应用，虽然完成了工程任务，但对其背后的机理尚存一知半解。恰逢项目告一段落，我决定重新梳理相关理论。
本文主要基于 MIT 课程 6.S184 的内容，结合个人的理解整理而成。如有偏颇之处，欢迎指正交流。

1. Flow Models：从直觉到定义

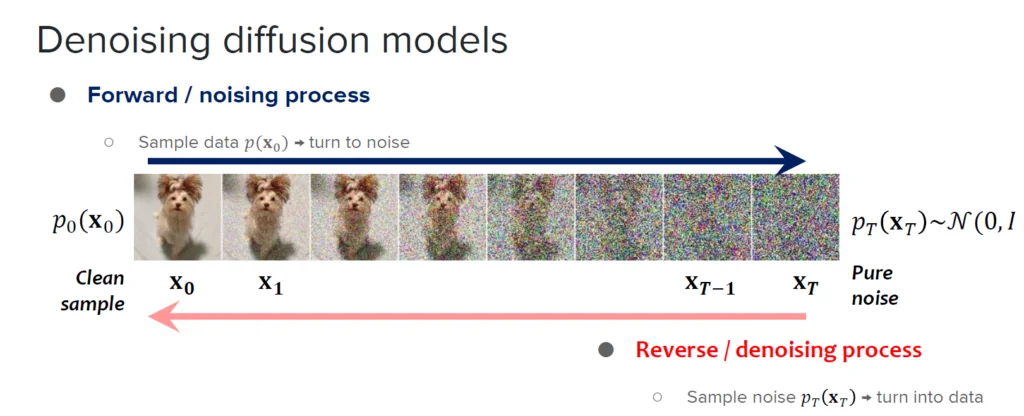
我们在图像生成领域对生成式模型（Generative Models）通常有一个直观的印象：模型从一个简单的先验分布（通常是高斯噪声，$x \sim \mathcal{N}(0, I)$）出发，经过逐步的去噪过程，将其转化为符合真实数据分布的样本（如下图粉色箭头所示）。

diffusion_on_image

为了在 Flow Matching 的框架下严谨地讨论这个问题，我们首先对符号进行统一定义（注意：此处符号习惯遵循 Flow Matching 常用设定，与经典 DDPM 可能相反）：

$$ \begin{align} & t : \text{时间变量，} t \in [0, 1] \\ & x_t : \text{生成过程中的中间状态} \\ & x_0 : \text{源分布（Source Distribution），即初始噪声} \\ & x_1 : \text{目标分布（Target Distribution），即真实数据} \end{align} $$

1.1 向量场与 ODE (常微分方程)

从零开始思考生成过程：给定当前状态（如噪声图）$x_t$，我们需要一个机制来指导我们进入下一个时刻的状态 $x_{t+\Delta t}$。
直觉上，我们希望存在一张“地图”，在任意时刻、任意位置都能告诉我们移动的方向和速度。为了简化问题，我们假设这个变化只依赖于当前状态 $x_t$ 和时间 $t$，而不依赖于更早的历史状态。

在数学上，这种瞬时的变化率可以用常微分方程 (Ordinary Differential Equation, ODE) 来描述：

$$ \begin{align} \frac{d}{dt}X_t = u_t(X_t) \\ X_0 = x_0 \quad (\text{初始条件}) \end{align} $$

这里的 $u_t(X_t)$ 就是我们所说的“地图”，学术上称为时间依赖的向量场(Time-dependent Vector Field)，或者速度场(Velocity Field)。

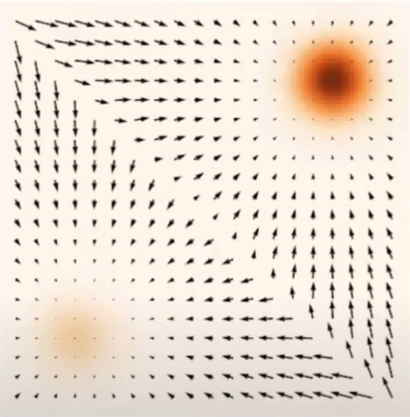
Dr. Yang Song 在其论文中给出了清晰的可视化：

vector_field

  • 直观理解：想象 $x_t$ 是平面上的一个粒子，图中的黑色箭头表示向量场 $u_t$。在任意位置 $x_t$，向量场指导粒子以特定的速度和方向移动到下一个位置。
  • 求解过程：生成数据的过程，本质上就是给定初始噪声 $x_0$，沿着向量场 $u_t$ 积分求解 $x_1$ 的过程。

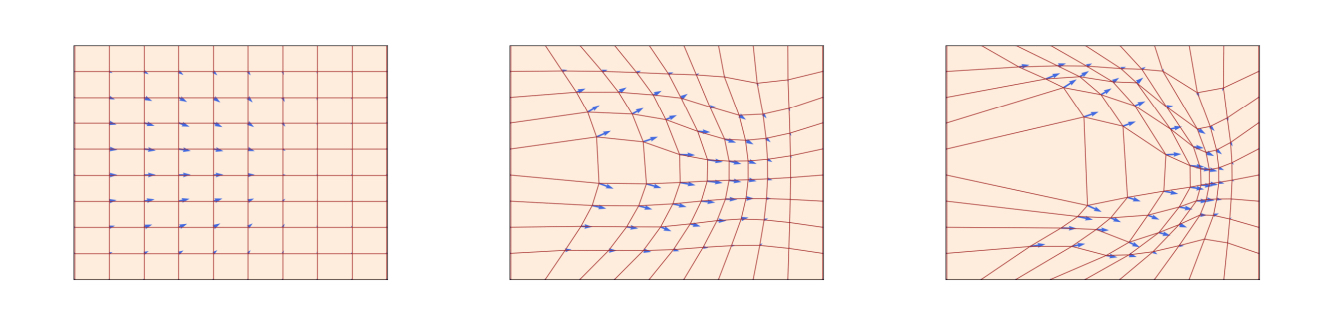
下图展示了在时间维度上，粒子如何跟随“地图”演变：

flows_on_time_dimension

基于此观察，Flow Models 的核心思想在于：如果我们能训练一个神经网络来拟合这个向量场 $u_t(X_t)$，那么我们就能通过求解 ODE，将简单的噪声分布 $p_{0}$ 平滑地推演变换到复杂的数据分布 $p_{1}$。

示例：线性向量场
假设一个简单的向量场 $u_t(X_t) = -\theta X_t$，我们可以直接求出解析解：
$$ \frac{dX_t}{dt} = -\theta X_t \implies X_t = e^{-\theta t}x_0 $$
验证：$\frac{d}{dt}(e^{-\theta t}x_0) = -\theta e^{-\theta t}x_0 = -\theta X_t = u(X_t)$。

1.2 ODE 数值解法 (Euler Method)

在实际应用中，神经网络拟合的 $u_t(X_t)$ 通常高度非线性，无法求出解析解。因此，我们需要使用数值方法进行近似求解，最基础的方法即为欧拉法 (Euler Method)。

欧拉法本质上是用离散的折线来逼近连续的曲线。选取步数 $N$，步长 $h = \frac{1}{N}$，对于给定的初始状态 $X_0$，迭代公式如下：

$$ X_{t+h} = X_t + h \cdot u_t(X_t) , \quad t \in \{0, h, 2h, \dots, 1-h\} $$

1.3 Flow Models 算法总结

至此，我们可以将 Flow Models 的生成过程（Inference）总结为以下算法：学习到一个向量场 $u_t$，并将简单分布 $X_0 \sim p_{\text{init}}$ 映射到目标分布 $X_1 \sim p_{\text{data}}$。

flow_model_ODE_simulate

2. Diffusion Models 与 SDE

在 Flow Models 中，我们构建了确定性的轨迹。对于固定的 $X_0$，生成的 $X_1$ 是唯一的。但在 Diffusion Models 的视角下，我们引入了随机性，这便涉及到了 SDE (随机微分方程)。

2.1 为什么引入 SDE？

从 ODE 到 SDE 的转变主要基于以下考量：

  1. 多样性与覆盖率：确定性的映射在某些情况下可能无法覆盖目标分布的所有模式（Modes）。
  2. 误差修正：在数值求解过程中，欧拉法会产生离散化误差。ODE 轨迹一旦偏离，无法自我修正；而 SDE 引入的噪声项（配合某些漂移项）可以起到“将偏离的轨迹拉回来”的作用，具有更强的鲁棒性。

2.2 SDE (Stochastic Differential Equation) 定义

我们将 ODE 中的确定性方程扩展为包含随机项的 SDE：

$$ \begin{align} dX_t &= u(X_t, t)dt + \sigma_t dW_t \\ X_0 &= x_0 \end{align} $$

其中：

  • $u(X_t, t)dt$ 是 漂移项 (Drift term)，对应原来的确定性向量场，控制整体运动趋势。
  • $\sigma_t dW_t$ 是 扩散项 (Diffusion term)， $\sigma_t$ 是控制噪声强度的系数。
  • $W_t$ 代表 布朗运动 (Brownian Motion)（或维纳过程 Wiener Process）。

直观上，布朗运动具有独立增量特性：对于任意 $0 \le s < t$，增量 $W_t - W_s$ 独立于过去的状态，且服从高斯分布：

$$ W_t - W_s \sim \mathcal{N}(0, (t-s)I) $$

2.3 SDE 数值解法 (Euler-Maruyama)

对应于 ODE 的欧拉法，SDE 的数值求解通常使用 Euler-Maruyama 方法。
给定漂移项 $u(X_t)$ 和扩散系数 $\sigma_t$，步长 $h = \frac{1}{N}$，更新公式为：

$$ X_{t+h} = X_t + \underbrace{h u(X_t)}_{\text{Deterministic}} + \underbrace{\sigma_t \sqrt{h} \epsilon_t}_{\text{Stochastic}}, \quad \epsilon_t \sim \mathcal{N}(0, I) $$

注意：随机项缩放系数是 $\sqrt{h}$ 而非 $h$，这是由布朗运动的方差性质决定的（$\text{Var}(dW) \propto dt$）。

注：Ornstein-Uhlenbeck (OU) 过程
值得一提的是，当漂移项为线性形式（如 $u(X_t) = -\theta X_t$）时，该 SDE 被称为 Ornstein-Uhlenbeck (OU) 过程。
$$ dX_t = - \theta X_t dt + \sigma_t dW_t $$
这种过程具有均值回归（Mean-reverting）的特性，常用于描述粒子在摩擦力作用下的布朗运动，也是许多 Diffusion 模型的前向过程基础。

2.4 可视化对比：ODE vs SDE

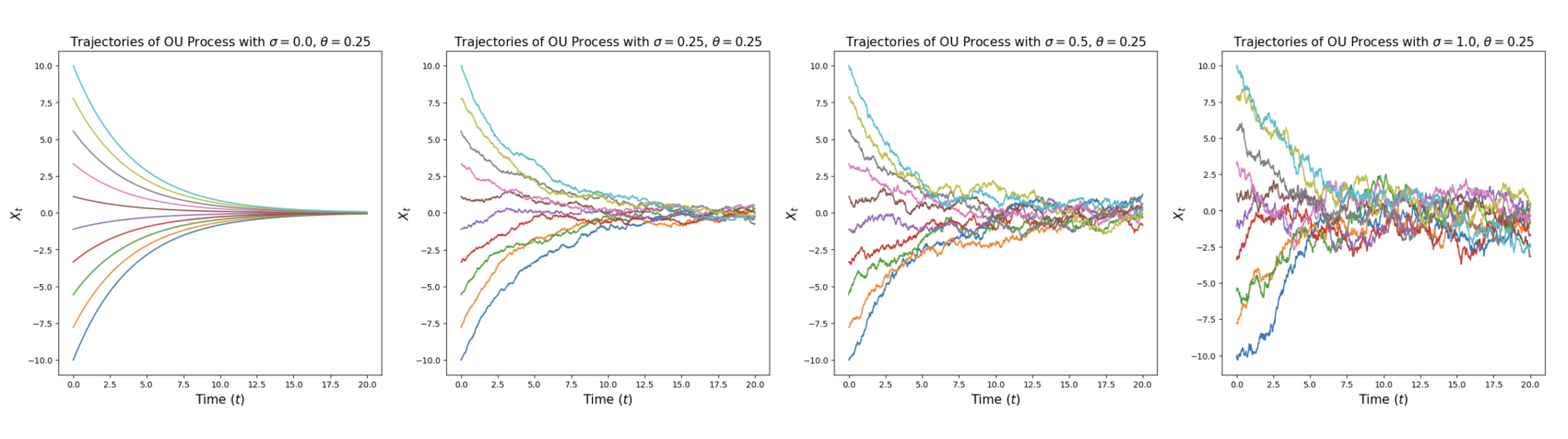
如果我们对上述例子进行可视化（如下图 Lab1 所示），可以直观地看到两者的区别：

  • ODE：轨迹平滑、确定，粒子沿着流线移动。
  • SDE：轨迹抖动、随机，粒子在宏观趋势上移动的同时，伴随着微观的布朗运动。

vis_ode_sde