构建训练目标

前言：
前文我们在假设向量场 $u_t(X_t)$ 已知的情况下，分别推导了 ODE 和 SDE 的前向过程。这一节我们将推导如何构建一个训练目标，让神经网络来学习。

假设神经网络 $u^{\theta}_{t}(x)$，我们有损失函数：

$$ \begin{align} \mathcal{L}(\theta) = \mathbb{E}_{t, x} \left[ \| u^{\theta}_{t}(x) - \underbrace{u^{target}_{t}(x)}_\text{training target} \|^2 \right] \end{align} $$

条件概率路径和边缘概率路径

如图所示，我们将初始分布（噪声）到目标分布（数字）做一个插值，就是一个概率路径。
interpolation_cond_path

在这个例子下，我们进一步描述：整个目标分布就是 0～9 的数字图像（MNIST）。假设我们采样了一张确切的图像 $z$（例如图中的数字 2）。

  • 一个从初始分布到目标样本 $z$ 的插值路径，被称为一个条件概率路径 $p_t(\cdot | z)$。
  • 一个从初始分布，到目标分布的所有条件路径的加权和，被称为边缘概率路径 $p_t(\cdot)$。形象地说，就是从初始分布到包含了所有数字图像的插值路径。

用数学表示来说，我们可以得到边界条件：
$$
\begin{align}
p_0(\cdot | z) = p_{init}, \quad p_1(\cdot | z) = \delta(\cdot - z), \quad \forall z \in \text{Dataset}
\end{align}
$$

理论上来说，当我们拥有足够多的采样点后，是可以得到边缘概率路径的：

$$ \begin{align} z \sim p_{data}, \quad x \sim p_t(\cdot | z) \implies x \sim p_t \\ p_t(x) = \int p_t(x | z)p_{data}(z) \mathrm{d}z \end{align} $$

遗憾的是：我们能够从目标分布中进行采样，但是不能确切得到 $p_t(x)$ 的值，因为上述积分没法进行（intractable）。
根据上文定义向量场的思想，我们只能尝试用神经网络来拟合一个向量场，间接完成从初始分布到目标分布的转换。于是我们有边缘向量场的定义：

$$
\begin{align}
X_0 \sim p_{init}, \quad \frac{\mathrm{d}}{\mathrm{d}t}X_t = u^{target}_t(X_t) \implies X_t \sim p_t \
u^{target}_t(x) = \int u^{target}t(x|z) \frac{p_t(x|z)p{data}(z)}{p_t(x)} \mathrm{d}z
\end{align}
$$

初见这个公式有些吓人，其实细细拆解一下也不难。依据贝叶斯公式：
$$
p(z|x) = \frac{p(x|z)p(z)}{p(x)}
$$
那么我们不难将 (6) 式变为：
$$
\begin{align}
u^{target}_t(x) = \int u^{target}_t(x|z) p(z|x) \mathrm{d}z
\end{align}
$$
依照数学期望公式，我们可以将 (7) 式进一步变为：

$$ \begin{align} u^{target}_t(x) = \mathbb{E}_{z \sim p(z|x)} [ u^{target}_t(x|z) ] \end{align} $$

我们仔细观察这个式子，从 MNIST 例子的视角下再解读一下：

  • $z \sim p(z|x)$ 提供的视角是：当前带噪声的图像 $x$ 可能是某个数字图像 $z$ 的后验概率（它是 1 的概率是 $w_1$，是 2 的概率是 $w_2$，…）。
  • 如果要生成数字 1，当前图像只需要沿着 $u^{target}_t(x|z_1)$ 走过去就好；生成数字 2 同理。
  • 只是现在没法确定我们要生成哪个样本，最理智的做法是：计算所有可能目标路径的加权平均（数学期望）。

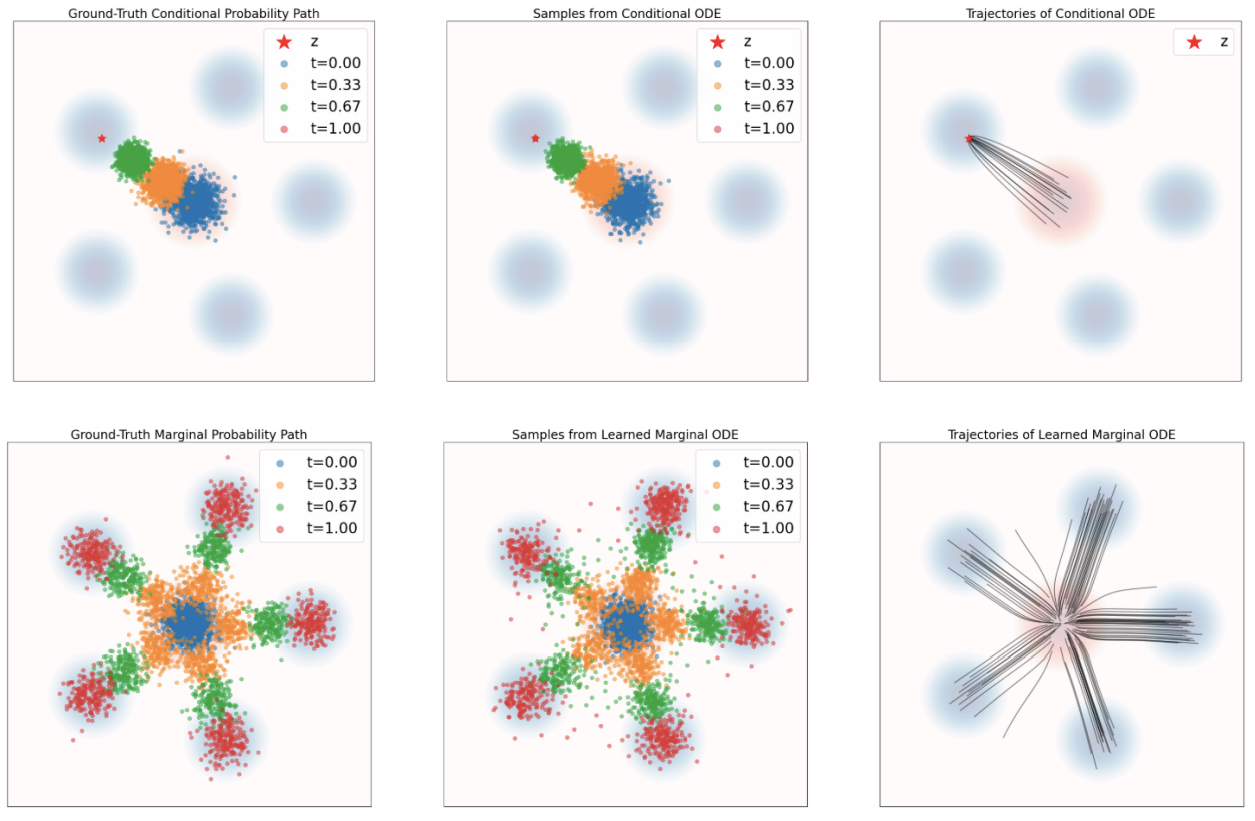
理解了上述的式子，我们可以直观形象地感受一下：
trajctory of u_target
图中第一行展示的是：当给定一个目标 $z$ 时，我们很容易从初始分布直勾勾地走向目标分布（条件概率）。
图中第二行展示的是：当我们对所有可能的 $z$ 进行加权（$z \sim p(z|x)$），我们能最终得到的概率路径（边缘概率路径）。

概率路径

前文反复提到了概率路径，一直只讲述了起点和终点，而没有介绍过程。实际上好的路径对目标向量场的求解也十分重要。
大多数 Flow Matching Model 和 Diffusion Model 使用的都是高斯概率路径。

设想一个高斯分布，其分布满足：$p_t(\cdot|z) = \mathcal{N}(\alpha_t z , \beta^2_t I_d)$，其中 $\alpha_t$ 和 $\beta_t$ 是提前设定的超参数（Noise Schedule），我们令：

  • $\alpha_0 = 0, \alpha_1 = 1$
  • $\beta_0 = 1, \beta_1 = 0$ (或趋近于0)

于是我们就有：
$p_0(\cdot|z) = \mathcal{N}(0, I_d), \quad p_1(\cdot|z) \approx \delta(\cdot - z)$

由高斯分布的特性，我们不难构造采样过程。引入标准高斯噪声 $\epsilon \sim \mathcal{N}(0, I_d)$，定义 Flow Map：
$$
\begin{align}
\psi^{target}_t(\epsilon | z) = \alpha_t z + \beta_t \epsilon
\end{align}
$$
显然，这样构造的 $X_t = \psi^{target}_t(\epsilon | z)$ 服从上述的高斯分布。

有了 Flow Map 的定义，我们尝试求解对应的条件向量场 $u_t^{target}(x|z)$。
根据向量场的定义：
$$
\begin{align}
\frac{\mathrm{d}}{\mathrm{d}t} \psi^{target}_t(\epsilon | z) &= u^{target}_t(\psi^{target}_t(\epsilon | z) | z) \
\dot{\alpha}_t z + \dot{\beta}_t \epsilon &= u^{target}_t(\alpha_t z + \beta_t \epsilon | z)
\end{align}
$$
为了得到 $u^{target}_t(x|z)$ 的表达式，我们需要把等式右边的 $\epsilon$ 用 $x$ 替换。
令 $x = \alpha_t z + \beta_t \epsilon$，则 $\epsilon = \frac{x - \alpha_t z}{\beta_t}$。代入上式：
$$
\begin{align}
u^{target}_t(x|z) &= \dot{\alpha}_t z + \dot{\beta}_t \left( \frac{x - \alpha_t z}{\beta_t} \right) \
&= \left( \dot{\alpha}_t - \frac{\dot{\beta}_t \alpha_t}{\beta_t} \right) z + \frac{\dot{\beta}_t}{\beta_t} x
\end{align}
$$
这正是我们需要的条件向量场公式（Conditional Vector Field）。

扩展到 SDE

前文我们在前向过程中从 ODE 添加布朗运动后，引入了 SDE。我们回顾一下 SDE 的形式：
$$
\begin{align}
\mathrm{d}X_t &= u(X_t, t)\mathrm{d}t + \sigma_t \mathrm{d}W_t
\end{align}
$$
一个形象的解释是：粒子知道当前时间步下应该往哪个方向走 ($u(X_t)$)，但是由于每一步走得都跌跌撞撞，有一些扰动（布朗运动导致的）。为了保持边缘分布不变，我们不得不添加一项修正：让每个粒子在走的同时，往目标概率密度最大的方向再做一个修正。我们将 SDE 的形式改写为：
$$
\begin{align}
\mathrm{d}X_t &= \left[ u^{target}_t(X_t) + \frac{\sigma_t^2}{2}\nabla \log p_t(X_t) \right] \mathrm{d}t + \sigma_t \mathrm{d}W_t
\end{align}
$$
其中 $\nabla \log p_t(x)$ 被称为 Score Function。

在高斯概率路径中，条件 Score Function 有解析解：
$$
\begin{align}
\nabla \log p_t(x|z) = \nabla \log \mathcal{N}(x; \alpha_t z, \beta^2_t I_d) = - \frac{x - \alpha_t z}{\beta^2_t}
\end{align}
$$
这意味着我们可以从 Score Function 中反解出 $z$：
$$
z = \frac{x + \beta_t^2 \nabla \log p_t(x|z)}{\alpha_t}
$$
将这个 $z$ 代入到之前推导的 ODE 向量场公式 (15) 中，我们可以发现 向量场 $u_t$ 与 Score Function 呈线性关系。

这意味着，在实际推理过程中，尽管 SDE 形式上多了一个修正项，但我们可以将其合并。我们不需要训练两个模型，只需要训练一个模型（无论是拟合 $u$ 还是拟合 Score），就能通过线性变换得到所需的全部项，完成推理。

总结：构建最终的训练目标 (The Training Target)

至此，我们完成了从理论推导到工程实现的闭环。我们构建训练目标的核心逻辑可以概括为：“想要的是边缘目标，训练的是条件目标”。

根据 Flow Matching 的理论（Marginalization Trick），拟合“简单的条件目标”在数学期望上等价于拟合“复杂的边缘目标”。因此，我们可以直接写出最终的 Loss 函数：

  1. ODE (Flow Matching) 训练目标：
    我们训练神经网络 $v_{\theta}(x_t, t)$ 去拟合条件向量场。对于高斯概率路径，这就是一个简单的线性回归：

    $$ \mathcal{L}_{FM}(\theta) = \mathbb{E}_{t, z, \epsilon} \left[ \| v_{\theta}(x_t) - u^{target}_t(x_t|z) \|^2 \right] $$

    其中 $u^{target}_t(x_t|z)$ 由公式 (13) 给出，本质上是在预测从噪声 $x_t$ 变回数据 $z$ 的速度方向。

  2. SDE (Score Matching) 训练目标：
    我们训练神经网络 $s_{\theta}(x_t, t)$ 去拟合条件分数函数。对于高斯分布，这等价于预测噪声（Denoising）：

    $$ \mathcal{L}_{SM}(\theta) = \mathbb{E}_{t, z, \epsilon} \left[ \| s_{\theta}(x_t) - \nabla \log p_t(x_t|z) \|^2 \right] $$

    其中 $\nabla \log p_t(x_t|z) = -\frac{x_t - \alpha_t z}{\beta_t^2}$，本质上是在预测噪声 $\epsilon$ 的反方向。

由于高斯路径下 $u_t$ 和 $\nabla \log p_t$ 存在线性关系，这两种训练目标本质上是互通的。我们完全可以使用 Flow Matching 的 Loss 训练一个模型，然后在推理阶段，通过公式变换，将其用于 SDE 的采样过程。这赋予了我们极大的灵活性：一次训练，既可确定性采样（ODE），也可随机性采样（SDE）。